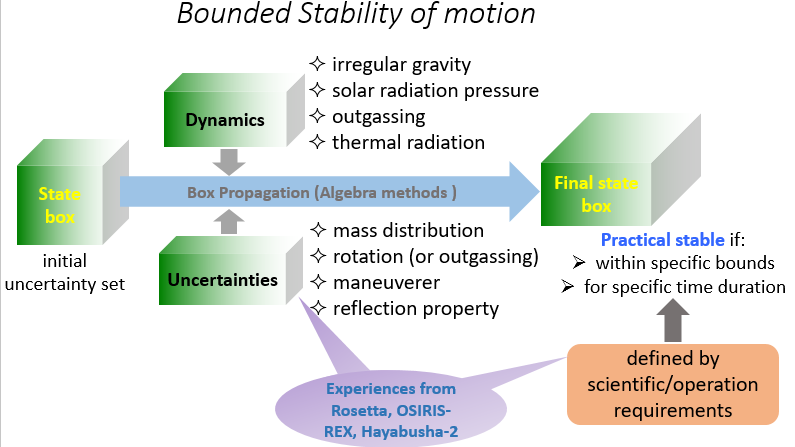
Explorations of minor bodies have attracted lots of attentions, in terms of their scientific and resource values, and also human safety concerns. One challenge for the mission design is to identify the stable motion of spacecraft (s/c) in the highly perturbed and uncertain dynamical environment. Many research focused on identifying the stable region under deterministic perturbations and using the Lyapunov stability criterion that is purely mathematical and cannot be well determined given uncertainties of either the initial state or model parameters. Therefore, considering both perturbations and uncertainties, this research presents an approach to statistically address the bounded stability region, where the s/c can stay within specific bounds for the specific time duration with the aim to meet the practical mission requirements. The uncertainties are divided into two categories: 1) with known/assumed distribution, e.g. the initial state, model parameters; 2) with known/assumed bounds including process noise, maneuverer errors. To balance accuracy and efficiency for facilitating the onboard autonomy, the semi-analytical methods that approximate the nonlinear dynamics with truncated power series algebra based on either Taylor expansion or Chebyshev interpolation, are explored to propagate uncertainties to obtain the state flow, from which the bounds are available for stability evaluation. Further, by comparing the bounded stability region with the deterministic Lyapunov stable region, the stability margin can be characterized. Moreover, the evolution and sensitivities of this bounded stability region to the variations of the perturbations and the uncertainty set (including magnitude and distribution) are investigated, from which the maximum uncertainties that the system can allow for bounded stability can be identified. Therefore, these analyses enhance the robustness of the mission design. A software tool will be developed for systematical analysis.