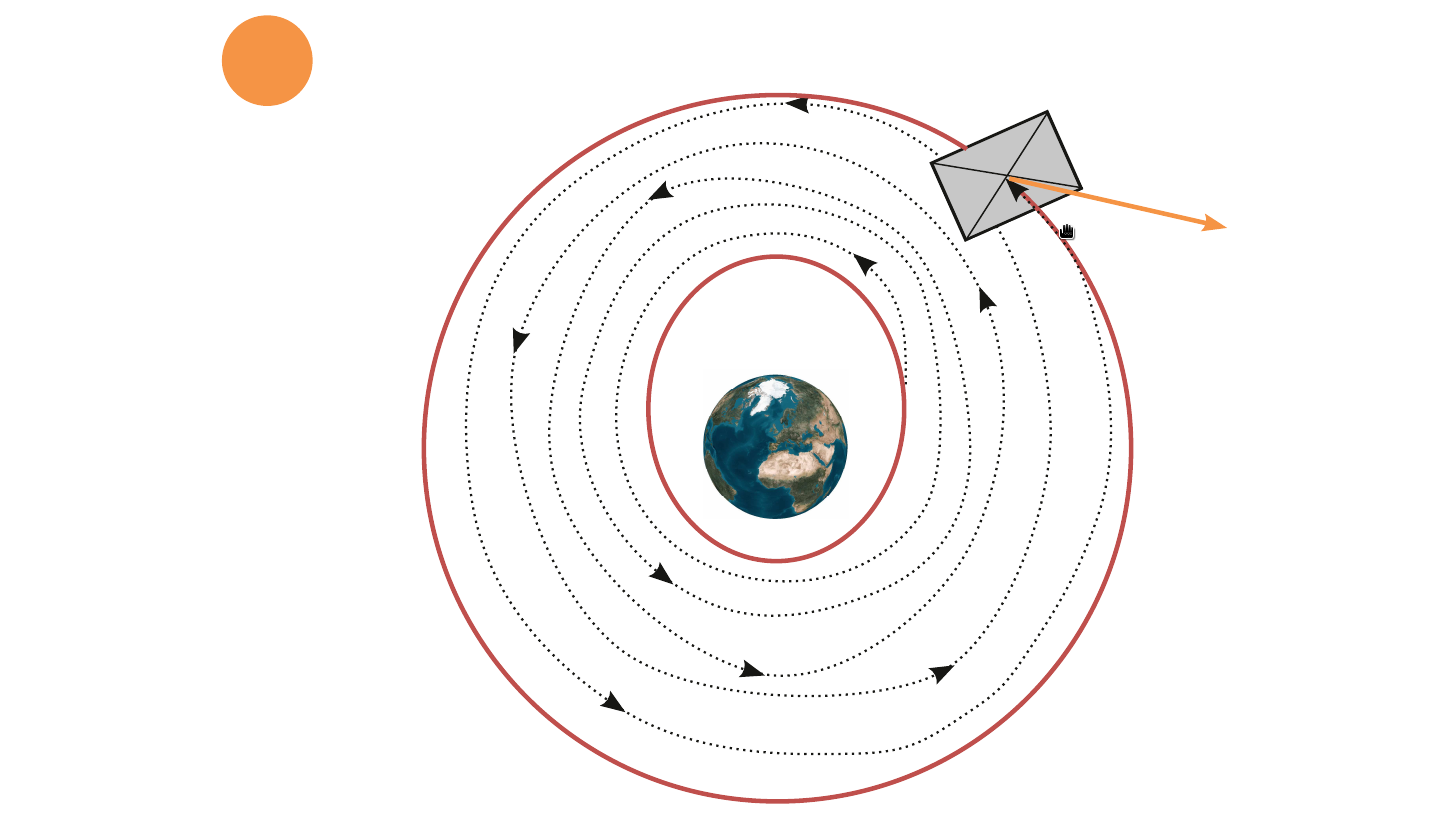
Solar sails enable ambitious and cost-efficient space missions to achieve interplanetary transfers, end-of-life disposal of LEO satellites, and space-based geoengineering. Optimal control theory was previously used to design interplanetary transfers, whose manoeuvring time is generally of the order of one heliocentric orbit. On the contrary, multi-revolution Earth escape or de-orbiting trajectories were addressed by means of sub-optimal feedback control laws, which do not lend themselves to the inclusion of precise initial or final conditions. Our research will focus on optimal (mostly minimum time) control methods for multi-revolution manoeuvres. The fast-oscillating nature of this problem causes severe technical difficulties to achieve a numerical solution, and this is probably why this path has not yet been followed. The innovation that we propose is the multi-phase averaging of the optimal control Hamiltonian of such manoeuvres (although averaging is extensively used in astrodynamics, direct averaging of the optimal control Hamiltonian is a rather recent technique). We carry out a full numerical evaluation of both the optimal control Hamiltonian and of the short-periodic oscillations (mean to osculating transformation). We use intensively shooting and automatic differentiation. The main objective of the research consists in applying this methodology and tools to solar sail control. Benefits are the parametrization of the optimal solution (i.e., manoeuvring time as a function of the sail size is available by solving a single averaged problem), broad understanding of the control strategy (at any time, the osculating solution is available for any Sun and satellite longitudes, which facilitates the identification of an optimal time window for the execution of the manoeuvre), and the possibility to include uncertain parameters in the analysis (because of the aforementioned flexibility).